Understanding Time Series Forecasting
Time series forecasting is a pivotal technique in predicting future events by leveraging historical data and insights into potential developments. This method involves the creation of LSTM models based on past data, which are then applied to make informed observations and guide strategic decisions for the future. Unlike general forecasting, time series forecasting specifically focuses on predicting values over a sequential period.
Establishing a time order dependence between observations introduces constraints and structural elements that offer valuable additional information. Essentially, the future is estimated by extrapolating from what has occurred in the past if historical trends will persist.
Real-world Applications of Time Series Forecasting
This technique finds widespread application across diverse fields, playing a crucial role in various domains such as finance, economics, healthcare and environmental science, where understanding and anticipating sequential patterns are essential for making well-informed decisions.
In finance, it aids in predicting Stock/Crypto prices and analysing market trends, empowering investors, and traders. Forecasting is important for disease outbreak predictions and hospital resource allocation in healthcare. Weather forecasting, manufacturing, transportation, telecommunications, and marketing also get benefit from this technique, shaping strategies and operations based on predictive insights.
Time series forecasting has proven essential in its ability to enhance efficiency, reduce uncertainties, and foster data-driven decision-making in the real world.
An Introduction to LSTM (Long Short Term Memory)
Long Short-Term Memory (LSTM) appears as a breakthrough in the field of artificial intelligence and machine learning, specifically designed for long-term dependencies within sequential data. As a type of recurrent neural network (RNN), LSTMs have gained prominence for their exceptional ability to model intricate patterns and relationships over extended sequences.
As information flows through layers during backpropagation, the gradients tend to either vanish or explode, hindering the effective learning of distant dependencies. This issue becomes particularly pronounced when dealing with sequences of varying lengths, as the impact of gradients diminishes exponentially over time.
Long Short-Term Memory (LSTM) networks were specifically designed to address the gradient problem in the context of sequential data processing.
How LSTM Differs from Traditional Neural Networks
Long Short-Term Memory (LSTM) networks differ significantly from traditional neural networks, particularly in their architecture and functionality, making them well-suited for tasks involving sequential data.
Memory Mechanism
Traditional Neural Networks: Traditional neural networks struggle with learning long-term dependencies in sequential data due to the vanishing or exploding gradient problem.
LSTMs: Long Short-Term Memory (LSTM) networks are Specifically designed to address this issue. LSTMs incorporate memory cells and gating mechanisms that enable them to selectively retain and forget information, allowing for the efficient modelling of temporal dependencies over extended sequences.
Sequential Dependency Handling
LSTM: LSTMs excel at capturing intricate sequential patterns and dependencies. The architecture’s ability to selectively update its internal state over time allows for efficient learning of temporal relationships.
Traditional Neural Networks: While traditional neural networks can handle sequential data to some extent, they may struggle with tasks that involve extended dependencies due to the vanishing gradient problem.
Applications in Time Series Forecasting
LSTM: LSTMs are widely used in time series forecasting because they capture and learn from historical trends and dependencies over time.
Traditional Neural Networks: While they can be applied to time series data, they may struggle to provide accurate predictions for sequences with long-term dependencies.
The Architecture of LSTM
Long Short-Term Memory (LSTM) stands as a specialized architecture within deep learning, functioning as a subtype of Recurrent Neural Networks (RNNs). It effectively tackles the issue of short-term memory limitations inherent in RNNs by introducing a cell state. This addition extends the duration for which past information can influence the network, enabling the retention of valuable insights from early elements in the sequence.
Comprising three crucial gates, the LSTM manages information flow as follows:
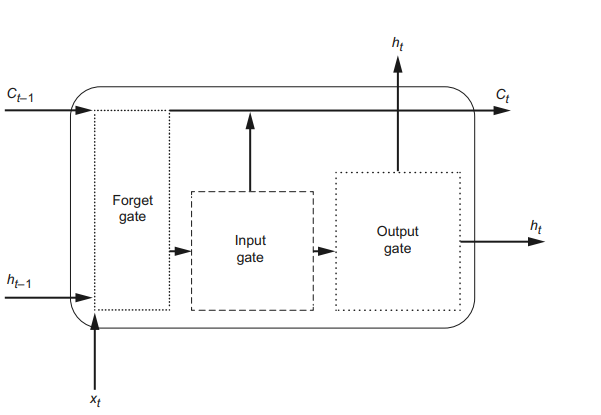
The forget gate assesses the relevance of information from previous steps.
The input gate determines the importance of information from the current step.
The output gate decides which information should be transmitted to the next sequence element or serve as an output to the final layer.
This intricate gating mechanism allows LSTMs to capture and retain long-term dependencies, making them highly effective in applications such as time series forecasting and natural language processing.
Why LSTM for Time Series Forecasting?
Enhanced Temporal Contextual Understanding
Long Short-Term Memory (LSTM) networks offer a different advantage in time series forecasting due to their capacity to comprehend and retain long-term dependencies. LSTMs integrate a cell state and gating mechanisms, enabling them to selectively incorporate historical information over extended sequences. This understanding is essential for capturing the nuanced patterns inherent in time series data, making LSTMs a preferred choice for accurate forecasting.
Adaptive Sequence Learning
LSTMs excel in the realm of time series forecasting by dynamically adapting to the nuances of sequential data. The network’s inherent ability to learn from temporal dynamics is facilitated by gating mechanisms that assess the relevance of past information at each step. This adaptive learning approach allows LSTMs to navigate through the sequential nature of time series datasets, providing a robust framework for capturing evolving patterns and making informed predictions.
Overcoming Short-Term Memory Constraints
Time series forecasting demands models that can effectively capture information from earlier segments of a sequence, a challenge for models with short-term memory constraints. LSTMs address this limitation by incorporating a cell state, ensuring that crucial historical information remains accessible over prolonged periods. This feature enables LSTMs to overcome the hindrances of short-term memory, delivering more accurate and insightful predictions.
Versatile Application Across Domains
LSTMs showcase their versatility in diverse time series domains, from financial markets to weather forecasting. Their adaptability to different datasets and the inherent capability to discern underlying patterns make LSTMs a versatile solution for a broad spectrum of time-dependent prediction tasks. This adaptability ensures that the model can effectively handle the unique challenges presented by various time series datasets.
Robust Handling of Varying Sequence Lengths
Time series data frequently exhibits varying sequence lengths, and LSTMs shine in their ability to handle this variability. The architecture’s inclusion of memory cells and gating mechanisms allows LSTMs to flexibly process sequences of different lengths, accommodating the real-world scenario where data may not conform to a standardized structure. This adaptability contributes to the model’s robust performance in a variety of time series applications.
Advantages of LSTM in Time Series Forecasting
Long-Term Dependency Handling: LSTMs work excellent at capturing and retaining long-term dependencies within sequential data, making them effective in forecasting time series with intricate patterns.
Vanishing Gradient Problem: The specialized architecture of LSTMs addresses the vanishing gradient problem, ensuring more stable and effective training over extended sequences.
Improved Short-Term Memory Handling: LSTMs overcome the limitations of short-term memory in traditional neural networks, ensuring the retention of valuable information from earlier elements in the sequence.
Efficient Learning from Historical Trends: LSTMs efficiently learn from historical trends, making them well-suited for applications where past information significantly influences future predictions.
Accurate Time Series Prediction: Overall, the advantages of LSTMs, including their ability to handle long-term dependencies and adapt to varying data lengths, contribute to their accuracy in time series forecasting applications.
Challenges of LSTM in Time Series Forecasting
Computational Complexity: LSTMs can be computationally intensive, especially in deep architectures or when dealing with large datasets, which may lead to longer training times and increased resource requirements.
Difficulty with Small Datasets: LSTMs may struggle to generalize well when dealing with small time series datasets, as they require enough diverse data to learn robust patterns.
Hyperparameter Tuning Sensitivity: Configuring optimal hyperparameters for LSTMs, such as the number of layers, units per layer, and learning rates, can be challenging, as the performance is sensitive to these settings.
Limited Effectiveness for Short Sequences: When dealing with very short time series sequences, LSTMs may not perform optimally, as they are designed to excel in tasks involving longer sequences with richer temporal dependencies.
Challenge of Feature Engineering: Efficiently selecting and engineering relevant features for LSTMs can be a non-trivial task, requiring domain expertise and careful consideration of the information that is most relevant for forecasting accurate results.
Preparing the Data for Time Series Forecasting
Data Collection
Initiating the time series forecasting process for Bitcoin price prediction involves a meticulous approach to data collection. To construct a comprehensive dataset, I have imported historical Bitcoin price data from the Coin Gecko platform.
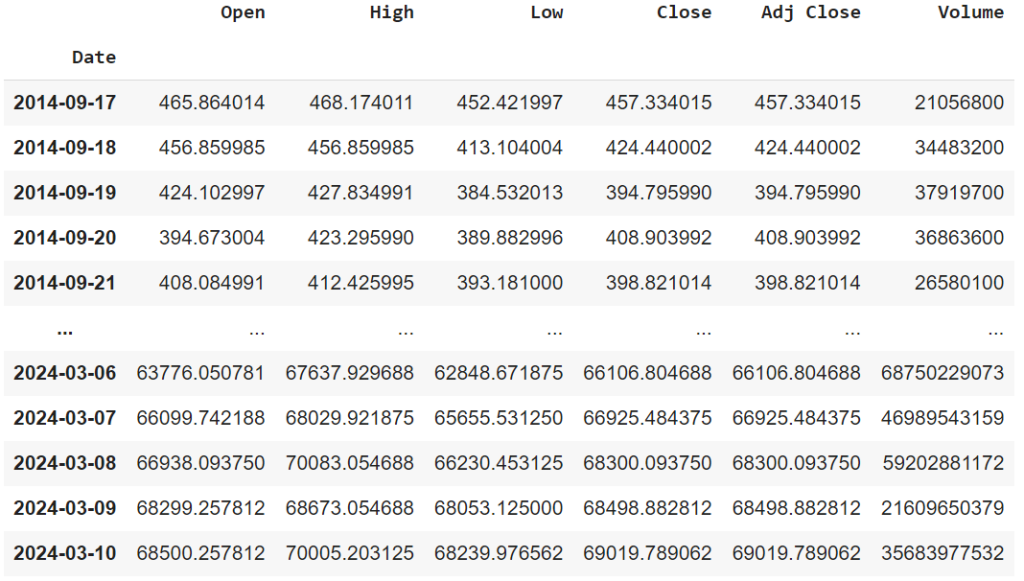
Utilizing reliable sources like Coin Gecko ensures access to accurate and up-to-date information, including timestamped price data and additional features influencing cryptocurrency markets. The dataset is curated with attention to detail, encompassing essential variables such as trading volume and market capitalization. This structured approach to data collection from reputable platforms sets the stage for a robust and informative dataset, laying the groundwork for accurate time series forecasting.
Data Pre-processing
Following the import of Bitcoin price data from Coin Gecko, the next crucial step involves data pre-processing. Adhering to specific rules ensures the data is suitable for time series forecasting. This includes addressing missing values, smoothing irregularities in the time series, and normalizing or scaling the data.
With a dataset sourced from Coin Gecko, it is essential to verify consistency and handle potential outliers or anomalies. The pre-processing phase also involves structuring the dataset to align with the requirements of the chosen forecasting model, facilitating seamless integration for subsequent analyses. By adhering to these pre-processing rules, the dataset becomes refined and conducive to training robust time series forecasting models.
By standardizing the data, the features are transformed to have a mean of zero and a standard deviation of one. This process is particularly beneficial when dealing with models that are sensitive to the scale of input features, as it ensures a consistent magnitude across all variables.
Standardization facilitates a more efficient optimization process during model training, preventing certain features from disproportionately influencing the learning algorithm. This, in turn, leads to improved model convergence and performance. By bringing all features to a common scale, standardization enables the model to better capture underlying patterns and dependencies in the data, ultimately contributing to higher accuracy in time series forecasting tasks.
Implementing LSTM for Time Series Forecasting
Setting up the Environment
Implementing Long Short-Term Memory (LSTM) for time series forecasting starts with setting up a conducive environment. This involves installing necessary libraries, such as TensorFlow or PyTorch, and ensuring that relevant dependencies are in place.
The environment setup should also encompass the configuration of key parameters, including the number of LSTM layers, units per layer, and other hyperparameters critical to the model’s performance.
Building the LSTM Model
Once the environment is configured, the next step is building the LSTM model architecture. This involves creating sequential layers of LSTM units, often accompanied by additional layers like Dense layers for output. The input shape and structure of the dataset are specified, ensuring compatibility with the LSTM model. Different gating mechanisms, such as input, forget, and output gates, are integrated into the model to capture and retain long-term dependencies. Careful consideration is given to the model’s complexity, balancing it to avoid overfitting or underfitting, and optimizing its architecture for effective time series forecasting.
Training the LSTM Model
With the LSTM model architecture in place, the training phase commences. The pre-processed Bitcoin price dataset is divided into training and testing sets.
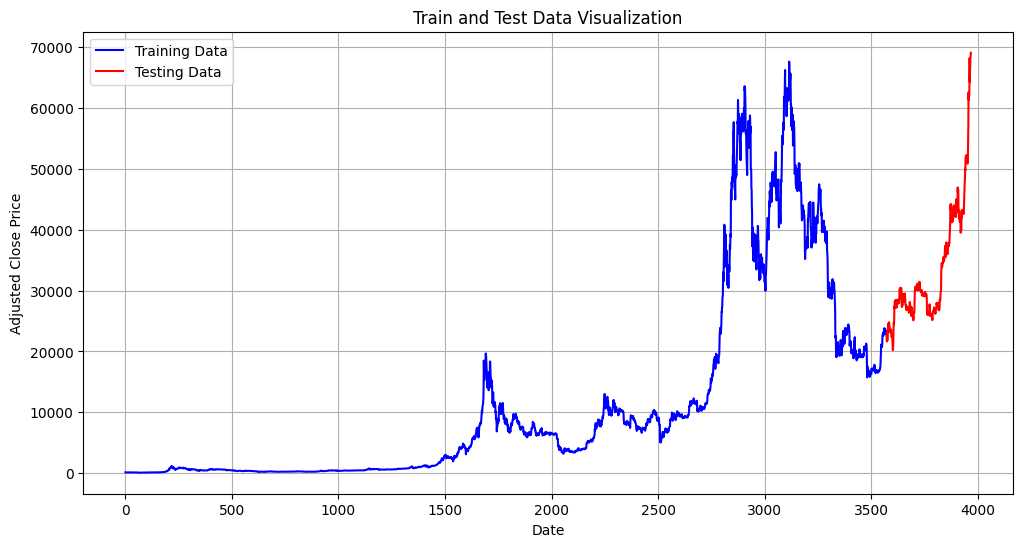
During training, the model learns to capture temporal patterns and dependencies from the historical data. The training process involves optimizing the model’s weights and biases through backpropagation and gradient descent. Model performance is continuously evaluated on the testing set to prevent overfitting and ensure generalization. Adjustments to hyperparameters may be made iteratively to enhance the model’s accuracy. The training phase concludes when the LSTM model demonstrates satisfactory performance in forecasting Bitcoin prices.
Evaluating the LSTM Model
To assess the effectiveness of the LSTM model in time series forecasting involves a comprehensive evaluation process. Key metrics and analyses are employed to measure the model’s accuracy, robustness, and overall performance. By comparing predicted values with actual observations, the model’s ability to capture temporal patterns and make precise forecasts is systematically evaluated.
Performance Metrics for Time Series Forecasting
To measure the LSTM model’s performance in numerical form, various metrics specific to time series forecasting are employed. Common metrics include Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and Mean Absolute Percentage Error (MAPE). These metrics provide insights into the model’s accuracy, how well it aligns with actual data points, and the extent of errors in predictions. We could also consider metrics such as R-squared or correlation coefficients can offer a comprehensive understanding of the model’s predictive capabilities.
Interpreting the Results
Interpreting the results of the LSTM model involves computing the performance metrics alongside visual inspections of predicted versus actual time series plots. A well-performing model should exhibit low error metrics and closely align predicted values with the true observations. Examining any discrepancies between predicted and actual trends allows for insights into potential model limitations or areas for improvement. A robust interpretation of results considers both quantitative metrics and qualitative assessments to ensure a holistic understanding of the LSTM model’s forecasting efficacy. Regular refinement and validation against new data further enhance the model’s interpretability and reliability.
Improving the Accuracy of LSTM Model
Enhancing the accuracy of an LSTM model involves a systematic approach to tuning and refining its parameters. Iterative adjustments are made to the model’s architecture, hyperparameters, and training process to achieve optimal performance. This phase is crucial for fine-tuning the model’s ability to capture complex patterns and dependencies within the time series data, ultimately leading to more accurate forecasts.
Tuning the LSTM Model
Tuning the LSTM model requires a careful exploration of hyperparameters and architectural configurations. Parameters such as the number of layers, units per layer, learning rate, and dropout rates are systematically adjusted. This iterative process involves training the model with various parameter combinations and evaluating performance metrics, such as Mean Absolute Error (MAE) or Root Mean Squared Error (RMSE). By fine-tuning these parameters, the model can adapt more effectively to the specific characteristics of the time series data, resulting in improved forecasting accuracy.
Incorporating Additional Features
To further enhance accuracy, consideration is given to incorporating additional features beyond the primary time series data. External factors or relevant indicators may be introduced to provide the model with more context for forecasting. These additional features could include economic indicators, sentiment analysis scores, or other relevant variables. The careful selection and integration of supplementary features contribute to a more comprehensive understanding of the underlying dynamics, empowering the model to make more informed predictions.
Predicting Future Points in Time Series using LSTM
To predict future points in the time series, use the trained LSTM model. Input the most recent historical data and allow the model to generate predictions for future points in the sequence. Iterate this process to generate a sequence of future predictions.
Post-process the predicted results, if necessary. This involves inverse transformations, denormalization, or other adjustments to bring the predicted values back to their original scale or format.
Attached is a visualization of the forecasted values alongside the actual ‘Adj Close’ prices. It’s important to note that, at this stage, our primary emphasis is on showcasing the forecasting process rather than optimizing the model. The graph provides an overview of the forecasted prices in comparison to the actual prices. Further refinement and optimization steps will be undertaken to enhance the model’s accuracy in subsequent iterations.
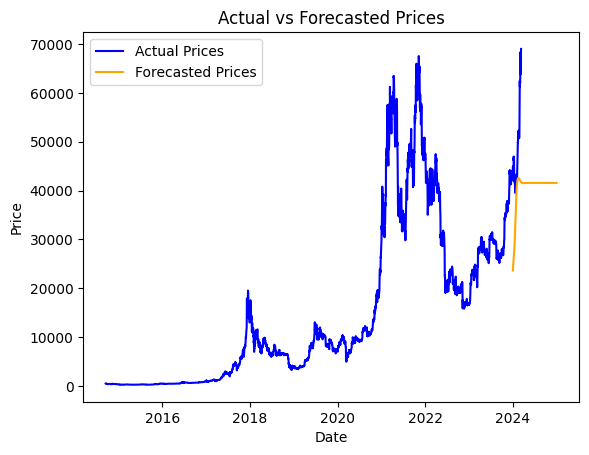
Interpretation of Predicted Results
To interpret the predicted values, We Begin by visually inspecting the predicted results alongside the actual time series data. Plot both the predicted and actual values on the same graph to observe the model’s performance in capturing trends and patterns.
Analyse the predicted results to identify patterns, anomalies, or trends. Consider whether the model successfully captures the inherent characteristics of the time series and whether the predictions align with expectations.
If necessary, iterate through the model training and prediction process to further refine accuracy. This may involve adjusting hyperparameters, incorporating additional features, or expanding the training dataset.
Finally, use the interpreted predicted results for decision-making. Whether it’s financial forecasting, resource planning, or other applications, leverage the insights gained from the LSTM model to inform strategic decisions based on anticipated future trends in the time series.
Is LSTM the Future of Time Series Forecasting?
- LSTM has showcased remarkable adaptability across various domains, including finance, healthcare, energy, and more. Its ability to capture intricate temporal dependencies positions it as a versatile tool for a wide range of time series forecasting applications.
- The inherent design of LSTM, with its memory cells and gating mechanisms, makes it particularly effective in capturing and retaining long-term dependencies within sequential data. This feature is crucial for forecasting tasks where historical context significantly influences future trends.
- Ongoing research and advancements in LSTM architectures contribute to their evolving capabilities. As researchers continue to refine and enhance LSTM models, they are likely to remain at the forefront of innovative time series forecasting techniques.
- LSTM models support end-to-end learning, allowing them to automatically learn relevant features from the input data. This characteristic simplifies the modelling process, making LSTM a candidate for tasks where feature engineering can be challenging.
- With the availability of open-source libraries and frameworks, the implementation of LSTM models has become more accessible to a broader audience. This democratization of technology fosters widespread adoption and experimentation, contributing to LSTM’s potential future prominence in time series forecasting.



